EXCELマクロ・分子模型

VBA でグラフィック

Home 人工雪 雪結晶 雪氷景色 過冷却水 大気光学現象 実験・観察 グラフィック

はじめに

EXCELマクロやPAWER POINTマクロで、自分が好きな物を作っています。 大気光象計算EXCELは自分の撮った写真のチェック用に作り始めましたが、 できたころには出現位置や見え方を覚えてしまいました。

分子模型はPAWER POINTで描いたものをgifアニメにしています。 そしてフラクタルではEXCELマクロで描いたマンデルブロ集合やジュリア集合、 コッホ曲線の動画や画像を紹介しています。

おねがい

EXCELマクロおよびPOWETPOINTマクロについて

• 常識の範囲内で使用できる方のみ利用を許可します。
• 著作権は放棄しておりませんので、無断での二次配布、プログラム改変はご遠慮ください。
• その他、一般的なソフトのルールを順守してください。
• マクロが苦手な方はご遠慮ください。
• EXCELやPOWERPOINTファイルを実行した時に起きるいかなる不具合に対しても当方は責任を負えません。 というのも、マクロ自体に不備がないにもかかわらず、EXCELやPowerPointが異常な動作を行うことがあり、 制作側としては対処のしようがないためです。
• IE等のビューアーでは正常に動作しません。必ずダウンロードし自身のパソコンにあるファイルから実行してください。

マクロソフト

■EXCELマクロ

---

大気光象VBA

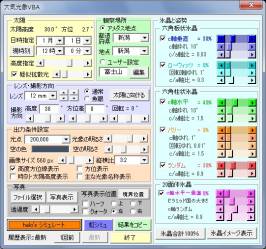
空に浮かぶ氷晶を透明な六角柱で表現し、 平たい六角柱（六角板状氷晶）・細長い六角柱（六角柱状氷晶）などに太陽光を当てたときの光の進み方を 反射・屈折の原理に従って計算することで、様々な大気光象をシミュレートするものです。 ご自身が撮られた大気光象をすぐにシミュレートするのは難しいと思いますが、 写真とシミュレート結果を重ね合わせながら、氷晶の形と姿勢を試行錯誤してみてください。

ファイルを開くと自動でマクロが動き、操作パネルが表示され、EXCEL自体は最小化されます。 何も設定しなくても「halo's シミュレート」ボタンを押せば、とりあえず大気光象シミュレート画像が表示されます。

申し訳ありませんが、操作説明書はありません。ボタン等へマウスオーバーした時に出る説明をみて操作してください。 エラーが出た状況等、メールで教えて頂けると助かります。いまだ不具合がありますので、 古いVerをお使いの方は必ず新しいVerに入れ替えてください。

大気光象の形の変化・YouTubeで見る

※大気光象VBAの公開版にに動画作成機能はついておりません。

新潟市の夏至の一日をシミュレートした動画です。主だった大気光象が一通り見られるような氷晶雲でシミュレートしています。

更新履歴

---

大気光象計算EXCEL

大気光象の出現位置や形状をEXCELのグラフで再現します。ダウンロードしてお楽しみください。なお、ファイルはzip形式で圧縮されています。

EXCEL2007以降対応です。EXCEL2003以前のバージョンでは動作しません。

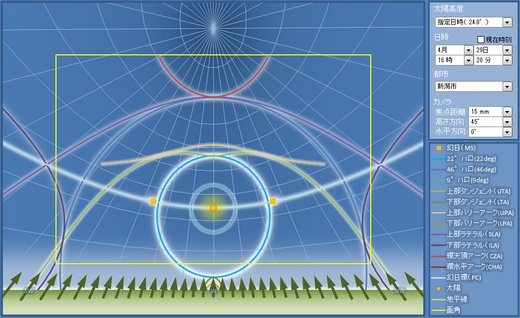
幻日・22°ハロ・46°ハロ・タンジェントアーク・ラテラルアーク・環水平アーク・環天頂アーク・幻日環、パリーアークが計算されます。 光が届くすべての範囲（入射角90°までと射出角90°（全反射）まで）を描いているので、実際の見え方とは異なります。出現する位置や形状の確認にお使いください。

＜使い方＞

「カメラ画角」「魚眼」「半球投影（ウルフネット）」「写真重ね合わせ」のシートがあります。「半球投影（ウルフネット）」以外には以下のプルダウンボックスで条件を指定して大気光象を再現します。

• 太陽高度：任意の太陽高度を指定します。また、”指定日時”を選択すると、任意の日付時刻の太陽高度を自動的に選びます。
• 日時にある4つのボックス：月、日、時、分をそれぞれ指定できます。
• 現在時刻：チェックを入れるとパソコンの現在時刻となります。月、日、時、分の指定は無視されます。
• 都市：観察したい最寄の都市を選択します。
• 焦点距離：35㎜換算でのレンズ焦点距離による大まかな画角（黄色枠、消すこともできる（後述））を指定します。
• 高さ方向：視点中央の高度を任意に指定します。太陽、幻日などを指定するとそれを中央にします。 このとき水平方向の指定値は無視されます。
• 水平方向：視点中央の太陽に対する方向を指定します。

「写真重ね合わせ」のシートではさらに以下の操作ができます。

• 画像挿入：ファイルを開くウインドウが出るので、大気光象写真を選びます。
• 少し縮小：写真を少しだけ縮小します。
• 少し拡大：写真を少しだけ拡大します。
• 右回転：写真を少しだけ右に回転します。
• 左回転：写真を少しだけ左に回転します。
• 大気光象チェックボックス：チェックを入れると表示、外すと非表示となります。 画角の枠線、地平線もここで表示するかどうか設定できます。

「カメラ画角」「魚眼」「半球投影（ウルフネット）」「写真重ね合わせ」のシートはそれぞれ以下の通りの投影を行っています。

• 「カメラ画角」：通常のレンズで撮影した場合の様子を再現します。
• 「魚眼角」：円周魚眼レンズで撮影した場合の様子を再現します。全天での見えかたを確認する場合に便利です。
• 「半球投影（ウルフネット）」：ウルフネットによる半球投影で大気光象を再現します。
• 「写真重ね合わせ」：通常のレンズで撮影した場合の様子を再現します。

最低限の注意：

すべての大気光象の出現位置をワークシート計算させているため、一つの操作を行うたびに再計算を行います。 そのため、それなりに速いCPUのパソコンでも、操作後に結果が反映されるまでに少し時間がかかります。 また、稀にボックスやボタンなどの位置がずれたり、見えなくなったりする可能性があります。 どうやらEXCELのマクロを使っているうえで避けられない不具合のようです。もしそうなった場合は保存せずにEXCELを終了し、 再度EXCELを起動しファイルを開き直してください。グラフを「画面に合わせる」表示に設定していると崩れるようです。

---

コッホ雪片EXCEL

コッホ曲線（Koch curve）を三つ合わせたフラクタル図形「コッホ雪片」を描くEXCELマクロです。ダウンロードしてお楽しみください。

ダウンロードしたファイルを開くと自動で描き始めます。いろいろとパラメータを変更し、できる図形で新しいデザインを作り出してみましょう。

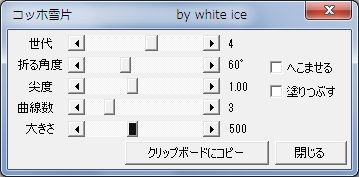
＜使い方＞

EXCELファイルを開くと操作フォームが出てきます。

• 「世代」：数値が大きいほど曲線が複雑に（コッホ曲線の世代が上がる）なります。
• 「折る角度」：コッホ曲線の中央部分の角度を指定します。
• 「尖度」：数値が大きいほど折られる山型部の大きさが大きくなります。
• 「曲線数」：組み合わせるコッホ曲線の数を指定します。
• 「へこませる」：チェックを入れると山型が内側にできます。
• 「塗りつぶす」：閉図形として描いているコッホ曲線の内部を塗りつぶします。
• 「大きさ」：描くサイズです。コピーした時の画像は大きさのピクセル数です。
• 「クリップボードにコピー」：描いたコッホ曲線をクリップボードにコピーします。
• 「閉じる」：コッホ雪片EXCELを終了します。

コッホ雪片の標準形は、折る角度＝60°、尖度＝1、曲線数＝3、「へこませない」です。 いろいろな雪結晶模様を描く場合は曲線数を6にするとよいでしょう。

最低限の注意：

EXCEL2000ではうまく動きません（全く描かれないわけではないですが…）でした。EXCEL2007と2010は動きました。2003以前は複雑な模様は描けません。「世代」というパラメータは、数が多くなるほど描画に時間がかかります。CPUのクロック数が 3GHzあっても少し待たなければなりません。あわてずに操作してください。

POWETPOINTマクロ

---

動く分子模型PPT

ファイルを開いた後、スライドショー開始→「マクロ開始」ボタンで右図のようなフォームが開きます。起動直後、エタノール分子がサンプルが描かれます。

あとは見た目で操作してみてください。まだベータ版です。回転アニメーションがうまく動かないPCがあるようです。

分子模型データであるSDFファイルやMOLファイルはしかるべき場所からダウンロードしてください。 原子数が300以下の分子に限ります。また、表示されない元素があります。

分子模型のgifアニメファイルは「動く分子模型」へ。

天体運動パワーポイント

重力に支配された天体の運動です。ケプラーの法則の理解にも役に立つでしょうか。

PowerPoint2003に合わせて作ったもので、2007以降だととても遅いです。PowerPointの仕様なので、どうしようもありません。 対応策としてEXCEL2007以降版に移植したのですが、需要がないと思われますので公開はしていません。

＜はじめ方＞

1. ツール→マクロ→マクロ→startを実行
2. スライドショー→実行→STARTボタンを押す

色々いじってみてください。裏技的動作が沢山あります。

最低限の注意：

PowerPoint 2007以降では本当に遅いです。フリーズしたかのように見えることもあり得ます。

■フラクタル

マンデルブロ集合（Mandelbrot set)、ジュリア集合（Julia set）、コッホ曲線（koch curve）による美しい絵や動画たちです。すべてEXCELマクロにより描いています。

マンデルブロ集合とジュリア集合のマクロの一般公開の予定はありません。EXCELマクロはマルチコアに対応せず、マルチスレッド処理できないので、マンデルブロ集合を計算するには速度が不十分です。

●マンデルブロ集合

複素平面上の関数 Z

漸化式： Z_k+1 = Z_k² + C ， Z₀ = 0

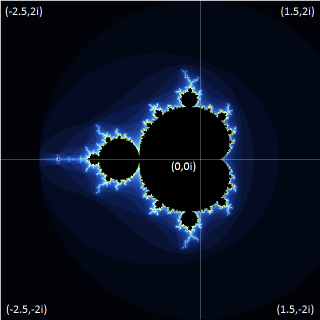
において、k → ∞ のとき Z が発散しない C 領域がマンデルブロ集合（右図で原点を囲む黒い領域）です。

発散した時の k の値によって色を塗り分けると、マンデルブロ集合の周りに美しい模様が描かれます。マンデルブロ集合以外の領域で美しい色模様ができ、マンデルブロ集合自体は複雑な輪郭線のみを作っていることになります。

また、2乗だけでなく、3乗、4乗・・・の場合もマンデルブロ集合を定義できます。

Z_k+1 = Z_kⁿ + C ， Z₀ = 0

こちらも美しい模様を描いてくれます。

動画

nはべき乗数、x、yは C の座標、zoom は拡大率（1の時x=±2、y=±2iの範囲）を示します。

n = 2
x=0.743907649209441
y=0.131712048105437
zoom=16,528,925,620 n = 2
x=0.0536421636064754E
y=-0.673572480898894
zoom=250,098,749.7 n = 2
x=-0.264457713095696
y=0.00286289445787072
zoom=200,182,584,402

静止画

VBAで複素計算のはなし

EXCEL VBAでは複素数計算ができないので、 Z と C を複素数 Z = x + yi 及び C = a + bi と置き、 複素平面座標で漸化式を実数軸と虚数軸を別々に計算させます。

Z_n+1 = （x_n + y_ni）² + a + bi = x_n² - y_n² + a + 2x_ny_ni + bi

→ 実数軸： x_n+1 = x_n² - y_n² + a 虚数軸：ｙ_n+1 = 2x_ny_ni + bi

VBAで書くと例えばこんな感じになります(x_k → x、x_k+1→xx という風に書き直してあります。）。ちなみにVBAではx ^ 2 よりも x * x と計算させるほうが処理が速くなります。

x = 0 : y = 0 ’初期値は0（Z₀ = 0）

 For a = amin To amax ’計算する実数軸範囲

  For b = bmin To bmax ’計算する虚数軸範囲

   For k = 1 To kmax ’無限まで計算できないので、kmaxまでの上限を設けます。

    xx = x ^ 2 - y ^ 2 + a

    yy = 2 * x * y + b

    If xx ^ 2 + yy ^ 2 > 4 Then Exit For ’半径2以内に集合があるので、それを超える→発散

    x = xx: y = yy ’kをひとつ進めます。

   Next

   If k = kmax + 1 Then

    Mandelbrot(a, b) = -1 ’kmaxまで発散しなければ、マンデルブロ集合内と判断

   Else

    Mandelbrot(a, b) = k ’発散した時のkを格納。

   End If

   x = 0: y = 0

  Next

 Next

これで、Mandelbrot(a,b) = -1 の座標を黒く塗ればマンデルブロ集合の完成です。 また、Mandelbrot(a,b)の値により色を塗り分ければ、綺麗なマンデルブロ集合図形が出来上がります。

●ジュリア集合

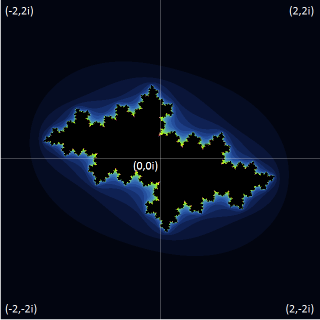
マンデルブロ集合、漸化式、Z_k+1 = Z_k² + C ，Z₀ = 0 において、k → ∞ のとき Z が発散しない C 領域でしたが、 ジュリア集合は漸化式、Z_k+1 = Z_k² + C において、 k → ∞ のとき Z が発散しない Z₀ 領域です。

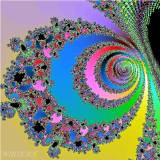
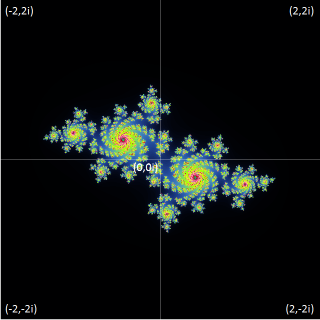
複素平面上の定数C（xj，yj）の位置により、ジュリア集合は大きく姿を変えます。C（xj，yj）がマンデルブロ集合内にあるとき、ジュリア集合が存在します。 下左図はC（-0.6，0.4）（マンデルブロ集合内の点）の時のジュリア集合（原点を囲む黒い領域）です。下右図はC（-0.6，0.45）（マンデルブロ集合の外の点）の時のジュリア集合周辺部の描く模様です。

マンデルブロ集合との関係

マンデルブロ集合に含まれる複素平面上の点をジュリア集合の定数C（xj，yj）にとると、 ジュリア集合は領域を持ちます。反対にマンデルブロ集合周辺の点を取るとジュリア集合は領域を持ちません（上の二枚の図を参照）。

マンデルブロ集合の周辺部の複素平面上のある点(x, y) をジュリア集合の定数C（x，y）とし、 (x, y)周辺の模様をそれぞれ描くと、似たような模様が浮かび上がります。

動画

n はべき乗数、xj、yjは Z₀ の座標、x、y は Z₀ の座標、zoom は拡大率（1の時xj=±2、yj±2iの範囲）を示します。

n = 6 xj=-1.1282 yj=0
x=0.573413286440667
y=0.993180945850281
zoom=100,000,000,000,000

静止画

n = 2 の標準的なジュリア集合を拡大したもの。

定数、座標を忘れると、二度と同じ模様を見れないかもしれません。

●コッホ曲線（koch curve）・コッホ雪片

1. 一本の直線を三等分し、真中の部分に三等分の線分を一辺とする正三角形を書きます。
2. 正三角形の底辺（元の直線の真中部分）を消します。
3. すると4本の直線でできた山型の図形が描かれます。

上記操作を１セットとし、無限に繰り返していったときにできる図形をコッホ曲線と呼びます。無限に直線を分割するので、各直線の長さは 0、つまり曲線となります。

右の動画は上記 1 セットの操作を繰り返していったときの、コッホ曲線の変化の様子を示しています。何セット操作したかを「世代」で表してます。 6 世代以降は画像の解像度に埋もれて変化がないようになります。

コッホ曲線を3つ向かい合うように並べてできる図形は、その形が雪の結晶のように見えることからコッホ雪片 （せっぺん）と呼ばれます（左側）。

正三角形を作るように直線をふやすのではなく、頂角や辺の長さが異なる二等辺三角形を作るように直線をふやすと、 違った形のコッホ曲線を描くことができます。このようなコッホ曲線を6つ向かい合うように並べると、 より雪の結晶らしい図形を描くことができます（右側）。

静止画

g は世代数、r は元の線分と山型部分の線分の長さの比、a は山型部分の頂角、n は組み合わせたコッホ曲線の数を示します。

■動く分子模型

POWER POINTやEXCEL VBAで描いたものをgifアニメにしています。

水分子や二酸化炭素分子のように平面に原子が並ぶものは手作業でも比較的簡単に描けます。 これがメタン分子のように3次元となっているものは座標計算が大変になりますが、 ←分子を作る原子の座標は、SDF形式等のデータとして公開されています。 そこで、マクロによりそのデータから直接分子を描けるようにしました。 ショ糖など複雑な分子もあっという間に描けます。 ただし、原子数が多い分子は処理落ちしたり、ずれた位置に描画されたりするどうにもならない不具合があります。

分子模型を描くパワーポイントは動く分子模型PPTに置いてあります。

アニメーション・ダウンロード

分子の画像をクリックすると gif 画像が動きます。動かしてから「画像を右クリック→名前を付けて保存」で保存してください。

注：分子模型画像の利用は自由としますが、一応出典を書くなどマナーは守ってください。

窒素 N2＆酸素 O2

窒素（緑）と酸素（赤）

空気の主要物質の窒素と酸素です。

微妙に窒素の方が大きく（ファンデルワールス半径をもとにしているので、その比率 155：152）、酸素の方が重い（約 7：8）です。

空気中の存在比率は約78：21≒4：1なので、この動画で空気を表現するならば、窒素分子を4個と酸素分子1個を描いて、 それぞれをランダムに移動させる必要があります。 回転させながらランダム移動、それに加えて終わりのコマと最初のコマがつながるようにするのは困難です。

二酸化炭素 CO2

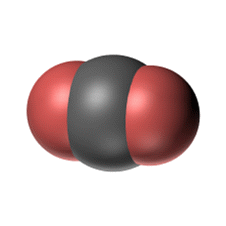
黒：炭素原子 赤：酸素原子

二酸化炭素は酸素−炭素−酸素と直線上に並んでいる分子で、原子のサイズを考えて 3D の奥行きを指定するだけで簡単に描けます。

地球温暖化の主犯にされていますが、そのほかのガスにも結構な温暖化ガスがあるので、二酸化炭素だけ悪者なイメージがありますが・・・ ある程度の二酸化炭素濃度は植物の成長を促進することもあり、植物には必要なガスですね。

氷Ⅰh

赤：酸素原子 白：水素原子

氷は非常に多くの結晶形を持っていますが、普通に氷を作るとこの氷Ⅰh という結晶形になります。 六方晶系で、雪の結晶はこの結晶形により六角形を基本とした形になります。

水分子（酸素[赤] 1 個と水素[白] 2 個）が、水素結合と呼ばれる結びつきで、立体構造をとります。 画像ではものすごく分子が詰まっているように見えますが、決まった方向から見るとかなりスカスカになっているのが確認できます。 液体の水よりも隙間が大きい→密度が小さく水に浮く、となります。

氷の結晶軸は a 軸と c 軸とがあります（ b 軸も定義されますが、a、c の 2 軸で表現されることが多いです）。 a 軸は互いに 120°で同一平面上で交わる a1〜a3 があります。 ちょうど正六角形の対角線方向です。c 軸は、すべての a 軸に対して直交する方向になります。

右の模型で、丸い穴が 7 個見え全体が六角形になる方向が c 軸方向、丸い穴が 9 個見え全体が長方形になる方向が a 軸方向となります。 ちなみにこの模型には水分子が 96 個あります。水素原子は隣り合う酸素原子の間に 1 個しかありません。

水 H2O

赤：酸素原子 白：水素原子

原子のサイズ（ファンデルワールス半径。水素1.2A（Aはオングストローム=10-10m）、酸素1.5A）、 共有結合距離（0.96A）、H-O-H 結合角104°です。

水分子は極性分子で、酸素がマイナス、水素がプラスの電気を帯びやすくなっています。 これらが引き寄せあうことで、固体である氷では水素結合を作ります。

エタノール分子 CH3CH2OH

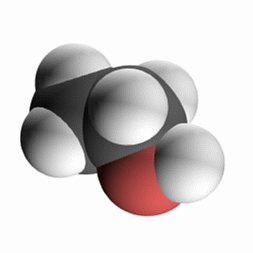
黒：炭素 赤：酸素 白：水素

注射前の消毒液の主成分ですね。蒸発しやすい液体で、殺菌効果があり、水のように結構いろいろなもの（特に有機物＝汚れ）を溶かすので、 皮膚に塗る→殺菌＆汚れを溶かす→一緒に蒸発→きれいに消毒される、ということで消毒に使われます。

エタノールのOH基（親水基）の水素原子と水分子の酸素原子、エタノールの酸素原子と水分子の水素原子がそれぞれ水素結合しやすいので、 水とは大変仲良し。どちらがどんな量でも溶け合います。さらに、溶かす前の合計体積よりも溶かした後の体積のほうが小さいという性質があります。

水は平面に3原子が並んでいるだけなので非常に簡単に描けますが、エタノールのように3次元に配置している分子は結構頭を使います。ところで、みなさん、エタノール分子は犬に見えませんか？

塩化ナトリウム NaCl

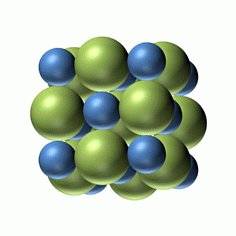
緑：塩化物イオンCl- 青：ナトリウムイオン Na+

食塩の主成分、海水の塩分の主成分、などなど、なじみのある塩化ナトリウムです。 寒剤としても有名で、氷水に食塩を溶かすと最低-21℃まで下げることができます。

結晶構造は面心立方格子で、図のように塩化物イオンは立方体の各頂点と各面の中心にあります。 同様にナトリウムイオンも各頂点と各面の中心にあります。 2原子が共に面心立方格子を形成している構造を、塩化ナトリウムを代表として岩塩型構造とも呼びます。

テトラクロロジベンゾパラジオキシン C12H4Cl4O2

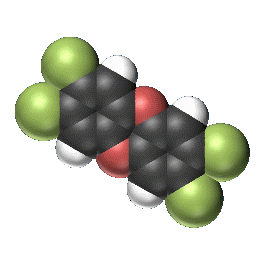
黒：炭素 赤：酸素 白：水素 緑：塩素 Cl

テトラクロロジベンゾパラジオキシン・・・代表的なダイオキシンのひとつです。

テトラ（ 4（個の））クロロ（塩素（に置き換わった））ジ（ 2（個の））ベンゾ（ベンゼン（環）） パラ（向かい合わせの位置）ジ（ 2（個の））オキシン（酸素）ということで、 ベンゼン 2 個（C6H6× 2 個）を基本として、 4 個の水素が 4 個の塩素に置き換えられ、4 個の水素の代わりに 2 個の酸素がベンゼンを結合しています。

ホウ酸 H3BO3

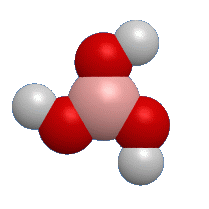
ピンク：ホウ素 赤：酸素 白：水素

殺虫剤などに使われている弱酸です。小学校の理科「もののとけかた」で、食塩や砂糖に並んで扱われることが多い試薬です。

ホウ酸の結晶も氷と同じく水素結合によってできています。

ショ糖（スクロース） C12H22O11

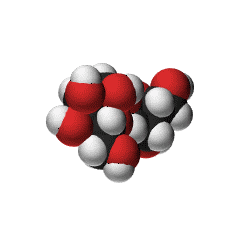
黒：炭素 赤：酸素 白：水素

砂糖の主成分です。見ずに良く溶ける（2.1g/g 25℃のとき）無色の物質です。

グルコース（ブドウ糖）とフルクトース（果糖）の分子がが結合した形をしており、二つの糖からなる二糖類です。

コレステロール C27H46O

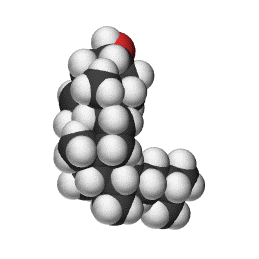
黒：炭素 赤：酸素 白：水素

コレステロールというと、善玉/悪玉とついて健康指標になっており、よく聞く名称です。 血液検査で出てくるコレステロールは、正確にはタンパク質分子との複合体で、純粋なコレステロール分子は細胞を作る主要な生体分子の一つです。

リモネン C10H16

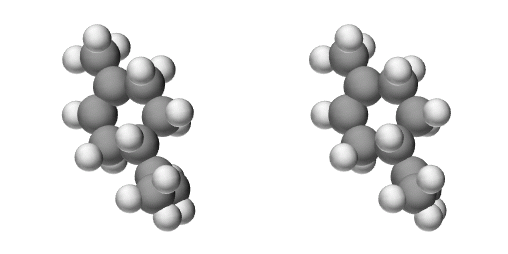
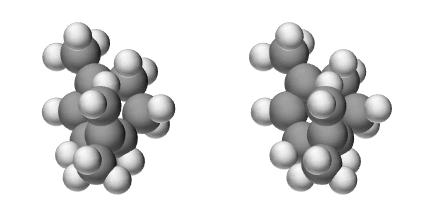
黒：炭素 白：水素

ミカンなどのかんきつ類の皮に含まれている、良い香りがする液体です。 ミカンの皮で油性マジックで描いた絵を消す実験がありますが、それはこのリモネンの性質です。 発泡スチロールを溶かす実験でも有名でしょうか。D体とL体があるので、それぞれ交差法のgifアニメを作ってみました。

光学異性体で、上がD体、下がL体です。

大気光象VBA 大気光象計算
EXCEL コッホ雪片
EXCEL 動く分子模型
パワーポイント 天体運動
パワーポイント マンデルブロ
集合 ジュリア集合 コッホ曲線 分子模型 ページトップ Home

cssはこちらを利用させていただきました。    Copyright (C) 20XX SITE NAME All Rights Reserved.　design by tempnate